Preliminary experiments for a time-domain brightness estimator based on negative feedback
The brightness of a sound is usually linked to the spectral centroid and is commonly obtained through FFT analysis and the calculation of a weighted mean of the magnitude of the frequency components. In order to have an accurate result using this technique a relatively large analysis window is necessary and, in some cases, it might be computationally too expensive and not ideal, especially if the project requires many of these units.
Di Scipio has already explored the idea of a brightness estimator in the time-domain in his Ecosistemico Udibile n.2 (Feedback Study), in which he performs the estimation simply by dividing the spectrum into two parts and then calculating the difference between the energy content of the two regions to see if the overall content is more in the low or high frequency range.
I am currently on a bus heading to London and since the journey is relatively long, I decided to try out some possibilities with Pure Data as I am planning to use brightness analysis for the next projects. The preliminary results seem to be sort of satisfying.
The idea is very simple, and even in this case it is based on dividing the spectrum into two regions, although the splitting point here is variable and is dependent on the resulting energy difference between the two spectra, which is what creates the self-regulating mechanism that performs the estimation.
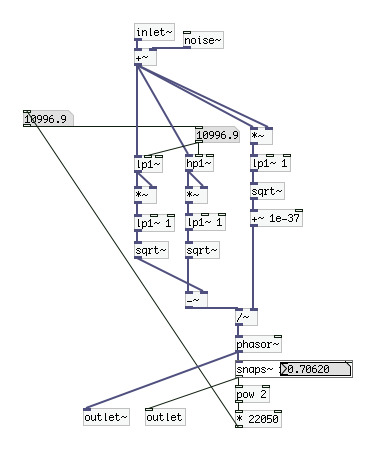
The input signal to be analysed is routed to a low-pass and high-pass filters whose cut-off frequency is linked. The RMS of the output of the two filters is calculated on a window of 1 second, and it is then calculated the energy difference between high and low spectrum. Intuitively, the cut-off frequency which results in a difference of zero is the spectral centroid of that signal, as the energy would be equally spread between the two parts of the spectrum. If the difference is a negative number there is more energy in the low region, if it is positive there is more energy in the high region, and this information can thus be used to shift the cut-off frequency of the filters towards either directions in order to counterbalance the difference. How great the difference is, instead, can be used as information on how much shift it is needed to cancel out the difference in the shortest time possible.
This kind of behaviour has been implemented by simply letting the energy difference drive the frequency of a phasor~ object - whose task is to linearly ramp out between 0 and 1 - and then by mapping the output of phasor~ to the entire frequency range to, in turn, set the cut-off frequency of the filters. A negative frequency will shift down, a positive frequency will shift up, and the greater the value of the frequency, the faster the shift will be carried out. This way, the system will find stability (although it will always be oscillating, even if for extremely small values) around a cut-off frequency which results in a zero-difference, indeed representing the centroid and brightness index of the signal.
The first issue encountered was the different responsiveness of the system with regard to different signals, namely to signals with different amplitudes. What I thought it could have been a work around was to normalise the RMS values out of the filters by using the RMS value of the input signal as a reference. Basically, the resulting difference is divided (avoiding zeroes) by the RMS of the input signal in order to keep the same range and have the responsiveness dependent on the relative energy difference rather than on the overall energy.
Lastly, the mapping between the phasor~ and the frequency range was chosen as a nonlinear one in order to have an index roughly closer to what the perception is.
In conclusion, with further refinements this might be a CPU-less-expensive extractor for brightness information which could be implemented with good results in some contexts, although the system becomes particularly non accurate in case the input signal has for example, and in the worst scenario, two sinusoidal components very far apart, which isn’t anyway something you would easily expect.